新型コロナウイルス感染者数をシミュレーション予測する
2020年8月10日
I-MR管理図とXBar-R管理図をつかって現状を分析する
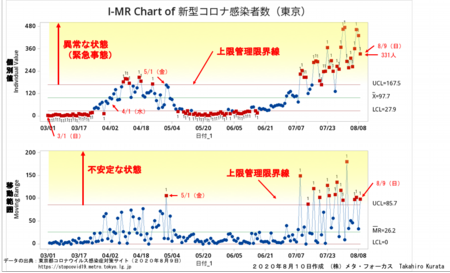
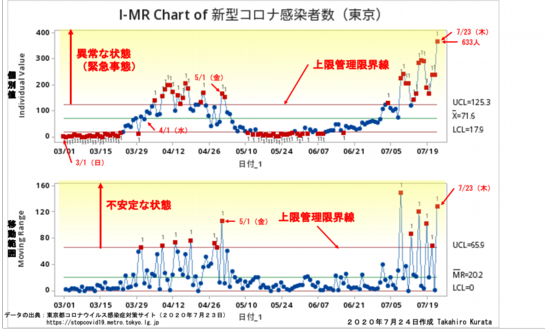
新型コロナウイルス感染者数の3/1からの推移をI-MR管理図を使ってプロットしたのが次の図です。自然なバラツキの範囲を超えて上昇傾向を続けているのがわかります。
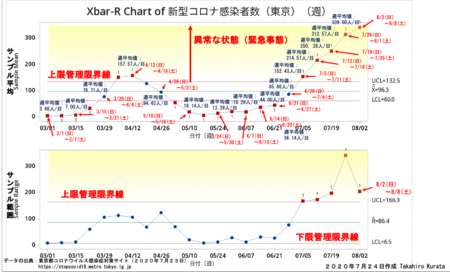
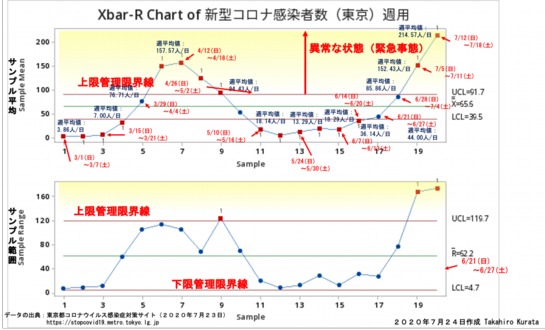
次の図はXBar-R管理図です。1週間の平均値の推移がプロットされています。週単位で見ても感染者数が確実に増加を続けているのがわかります。
回帰分析を使って感染者数の予測式を得る
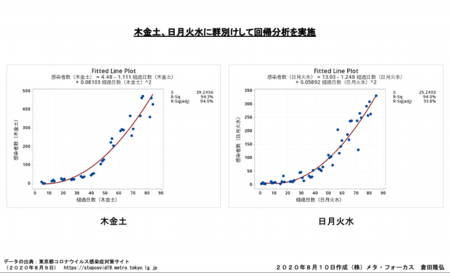
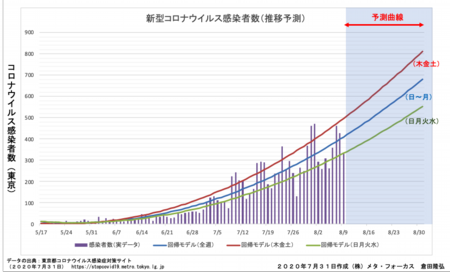
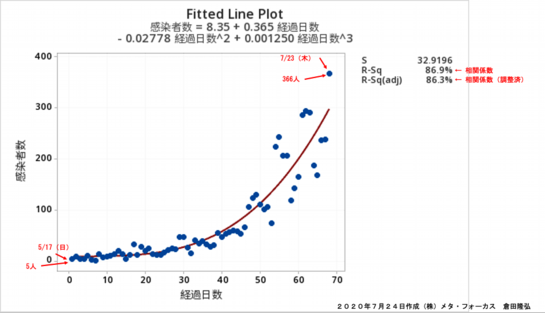
次の図は、木金土の感染者数と、日月火水の感染者数に群分け(グループ分け)してそれぞれの群の感染者数について回帰分析を実施した結果です。それぞれ90%以上の相関係数(R-Sq)が得られました。
次の図は回帰分析で得られた回帰式を使って8/9までの実データ(棒グラフ)と重ねて予測曲線としてプロットしたものです。
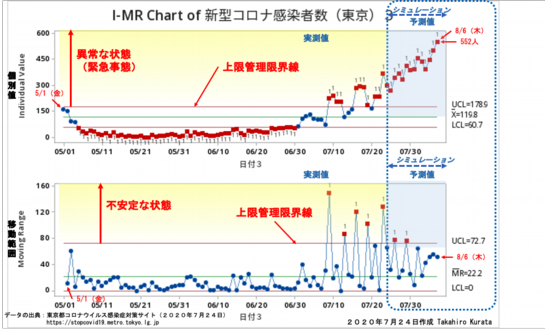
次の図は、木金土と日月火水に郡分けして得られた2つの回帰式を使って得られた予測値と乱数として生成した自然のバラツキの値とを合成してシミュレーションしたデータを I-MR管理図にプロットしたものです。
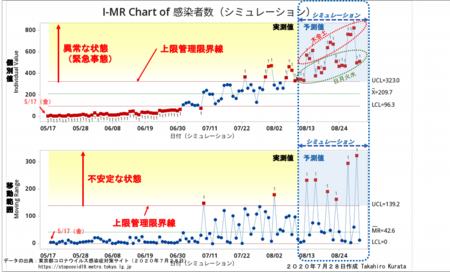
シミュレーションが外れて8月末に800人を超えない事を願っています。
新型コロナウイルス感染者数、(木金土)と(日月火水)に郡別けし検定分析し予測する
2020年7月29日
箱ひげ図(Box Plot)を使って曜日ごとの感染者数を見る
東京都における新型コロナウイルス感染者数には曜日によって繰り返すパターンがありそうなのでまずその全体像を箱ひげ図(Box Plot)を使って見て見ました。
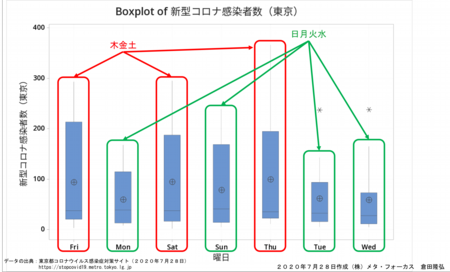
箱ひげ図から、木金土は日月火水に比べて数値が高くバラツキも大きいことが見て取れます。
そこで、木金土と日月火水に群別けしてみることにしました。
ヒストグラムを使って(木金土)と(日月火水)に群別けした感染者数の分布を見る
まずヒストグラムで木金土と日月火水の感染者数の分布を見てみました。
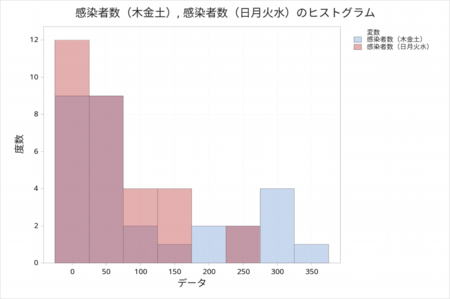
感染者数は指数関数的に増加し続けているので正規分布になっていないことが分かります。
Johnson変換を実施してデータ分布を正規化する
そこで、Johnson変換を使ってそれぞれの感染者数データを正規分布のデータに変換しました。
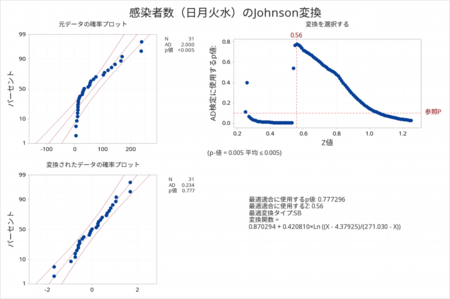
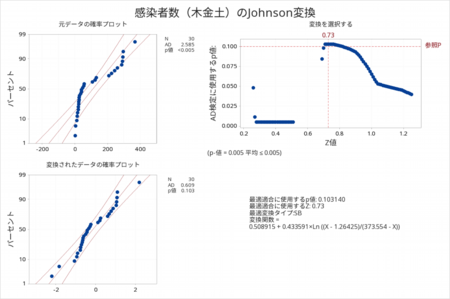
正規分布にデータ変換できているかヒストグラムで分布を確認しました。
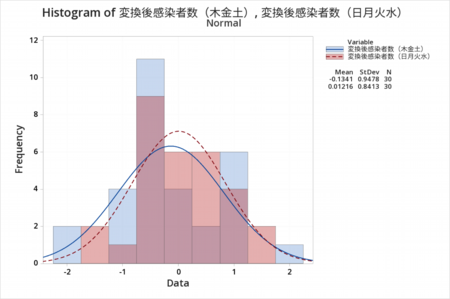
正規分布へのデータ変換がうまく行きました。
仮説検定を実施して(木金土)の感染者数と(日月火水)の感染者数に有意差があるかを確かめる
では、(木金土)の感染者数と(日月火水)の感染者数に有意差があるのかどうかを仮説検定を使って確かめて見ましょう。
この場合他比較対象の感染者数データは東京都という母集団に対して同じ環境でPCR検査が実施された結果ですから、対応のあるT検定(Paired T-test)を使います。
まず、仮説を立てましょう。
帰無仮説:感染者数(木金土) = 感染者数(日月火水)
対立仮説:感染者数(木金土) ≠ 感染者数(日月火水)
帰無仮説はそれぞれの感染者数に有意差がないということを示していて、対立仮説はそれぞれの感染者数には違いがあると言うことを示しています。
つまり、帰無仮説が棄却されて対立仮説が採択されればそれぞれの感染者数には違いがあると言う結論になります。
有意水準αを決めます。
有意水準:α=0.05 としました。
有意水準とはもし帰無仮説を棄却したことが実際には間違い(過誤)である確率の閾値です。
有意水準αを 0.05 と設定したことで、もし帰無仮説を棄却することが間違いである確率が5%以下であれば間違い(過誤)である確率が十分に低いとして、帰無仮説を棄却することを選択します。
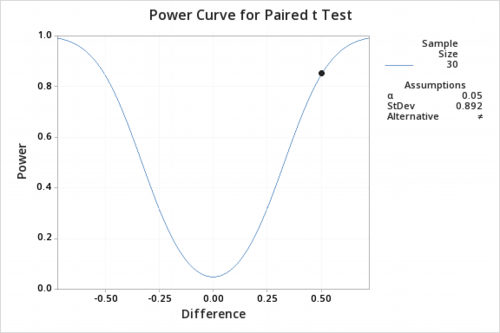
次に検出力(Power)を確認します。
まずは正規分布変換後のデータのバラツキを見るために標準偏差値を抽出しましょう。

サンプル数nは、n=30 です。
検出力(1-0.85)= 0.15 とすると有意差との関係は次のようになります。
では、帰無仮説を棄却したことが実際には間違い(過誤)である確率 P値を求めて見ましょう。

対応のあるT検定を実施した結果P値は、P値 = 0.036 となりました。
P値(0.036)< α値(0.05)ですので、帰無仮説を棄却することの間違い(過誤)の確率が十分に低いとして帰無仮説を棄却し対立仮説を採択します。
対立仮説:感染者数(木金土)≠ 感染者数(日月火水)
結論
木金土の感染者数と日月火水の感染者数には有意差があると言う事が統計的に確かめられました。
新型コロナウイルス感染者数の分析 - I-MR管理図
2020年7月27日
I-MR 管理図で感染者数の推移を分析する
新型コロナウイルス感染者数の、I-MR管理図を見ると感染者数は既に上限管理限界線を遥かに超えて緊急事態を示しています。気になるのがMR管理図で見るバラツキです。コロナウイルスの感染力が日々大きく変化するとは考えられないから、PCR検査や集計の状況が安定していない状況だと推測されます。なんらかの理由で第1波の時よりもバラツキが大きくなっています。
感染者数のバラツキの周期が1週間の曜日に関係しているとするとXbar-R管理図では1週間の平均値をプロットしているので日々のバラツキは吸収されています。こちらも週単位で見ると確実に急増しているのがわかります。
経過日数とともに日々のバラツキが大きくなっているので回帰分析の精度はやや低くなっていますがフィッティング度合いを示す相関係数(86.9%)は依然高いです。
モンテカルロ・シミュレーションではここ1〜2週間の標準偏差値よりは少し乱数のバラツキ(標準偏差値)に手加減を加えています。8月6日時点での予測式の算出結果は541人です。それに乱数によるバラツキを合成してのシミュレーション結果が552人となっていますが、実際にはバラツキはもっと大きいですから最悪の場合にはより大きな値になると思います。
 ホーム
ホーム